本笔记基于以下学习资料(侧重实际应用):
入门机器学习:(强推|双字)2022吴恩达机器学习Deeplearning.ai课程
Python 代码库:scikit-learn 官网
复习线性代数:3Blue1Brown 的 线性代数的本质 - 系列合集
统一口径
术语
- 特征(
feature):指输入变量; - 标签(
label):指输出变量,真实值(target或ground truth),预测值(prediction); - 训练集(
training set):用于训练模型; - 验证集(
validation set):用于防止模型过拟合; - 测试集(
test set):用于评估模型效果; - 训练示例(
training example):指训练集中的一组数据; - 模型(
model):指拟合函数或概率模型; - 模型参数(
parameter):调整模型的本质是调整模型参数; - 损失函数(Loss function):衡量预测值与真实值之间的差异程度,“单个损失”;
- 成本函数(
Cost function):用于评估模型性能,“总损失”; - 特征工程(
feature engineering):对特征进行选择、提取和转换等操作,用于提高模型性能;
符号
约定如下:
m个训练示例,n个特征;- $\mathbb{R}$ 表示
标量,$\mathbb{R}^n$ 表示向量,$\mathbb{R}^{m \times n}$ 表示矩阵,$\mathbb{R}^{m \times n \times p \times \cdots}$ 表示张量(Tensor);
具体符号:
- $x \in \mathbb{R}^n$ 表示
输入变量,$w \in \mathbb{R}^n$ 表示回归系数; - $X \in \mathbb{R}^{m \times n}$ 表示
训练集,$y,\hat{y} \in \mathbb{R}^m$ 分别表示真实值和预测值。- $x^{(i)} \in \mathbb{R}^n$ 表示第 $i$ 个训练示例;(第 $i$ 行)
- $x_j \in \mathbb{R}^m$ 表示第 $j$ 个特征;(第 $j$ 列)
- $x_j^{(i)} \in \mathbb{R}$ 表示第 $i$ 个训练示例的第 $j$ 个特征;
- $y^{(i)},\hat{y}^{(i)} \in \mathbb{R}$ 分别表示第 $i$ 个训练示例的真实值和预测值;
$$
x = \begin{bmatrix}x_1 \\ x_2 \\ \vdots \\ x_n \end{bmatrix}
\space
w = \begin{bmatrix}w_1 \\ w_2 \\ \vdots \\ w_n \end{bmatrix}
\space
y = \begin{bmatrix}y^{(1)} \\ y^{(2)} \\ \vdots \\ y^{(m)} \end{bmatrix}
\space
\hat{y} = \begin{bmatrix}\hat{y}^{(1)} \\ \hat{y}^{(2)} \\ \vdots \\ \hat{y}^{(m)} \end{bmatrix}
\space
$$
$$
X =
\begin{bmatrix}
x_1^{(1)} & x_2^{(1)} & \dots & x_n^{(1)} \\
x_1^{(2)} & x_2^{(2)} & \dots & x_n^{(2)} \\
\vdots & \vdots & \ddots & \vdots \\
x_1^{(m)} & x_2^{(m)} & \dots & x_n^{(m)}
\end{bmatrix}
\space
x^{(i)} = \begin{bmatrix}x_1^{(i)} \\ x_2^{(i)} \\ \vdots \\ x_n^{(i)} \end{bmatrix}
\space
x_j = \begin{bmatrix}x_j^{(1)} \\ x_j^{(2)} \\ \vdots \\ x_j^{(m)} \end{bmatrix}
$$
监督学习
回归任务,预测离散值的是分类任务。给定包含标签的训练集 $(X,y)$,通过算法构建一个模型,学习如何从 $x$ 预测 $\hat{y}$,即:$$ (X,y) \to f(x) \to \hat{y} $$
线性回归
线性回归(Linear Regression),解决线性的回归问题。
原理
模型
$n$ 元线性回归的模型 $f: \mathbb{R}^n \to \mathbb{R}$ 如下:
$$
f_{w,b}(x) = w \cdot x + b =
\begin{bmatrix}w_1 \\ w_2 \\ \vdots \\ w_n \end{bmatrix}
\cdot
\begin{bmatrix} x_1 \\ x_2 \\ \vdots \\ x_n \end{bmatrix} + b =
\sum_{j=1}^{n}w_jx_j + b
$$
其中,模型参数:
$w \in \mathbb{R}^n$:回归系数,分别对应 n 个特征的权重(weights)或系数(coefficients);
$b \in \mathbb{R}$:偏差(bias)或截距(intercept);
成本函数
使用最小二乘损失:
$$
\begin{split}
L(w,b) &= \frac{1}{2} (f_{w,b}(x^{(i)}) - y^{(i)})^2 \\
\\&= \frac{1}{2} (w \cdot x^{(i)} + b - y^{(i)})^2
\end{split}
$$
基于最小二乘损失,常见的三种成本函数:
$$ J(w,b) = \frac{1}{2m} \sum_{i=1}^{m} (f_{w,b}(x^{(i)}) - y^{(i)})^2 \tag{OLS} $$
$$ J(w,b) = \frac{1}{2m} \sum_{i=1}^{m} (f_{w,b}(x^{(i)}) - y^{(i)})^2 + \frac{\lambda}{2m} \sum_{j=1}^{n} \lvert w_j \rvert \tag{Lasso} $$
$$ J(w,b) = \frac{1}{2m} \sum_{i=1}^{m} (f_{w,b}(x^{(i)}) - y^{(i)})^2 + \frac{\lambda}{2m} \sum_{j=1}^{n} w_j^2 \tag{Ridge} $$
说明:
- 使用 $\frac{1}{2m}$ 取均值,仅是为了在求偏导时消去常数 2,不影响结果;
OLS:普通最小二乘回归;Lasso:Lasso 回归,用于特征选择。在 OLS 的基础上添加了 $w$ 的 L1 范数 作为正则化项;Ridge:岭回归,用于防止过拟合。是在 OLS 的基础上,添加了 $w$ 的 L2 范数 的平方作为正则化项;- $\lambda$:超参数,非负标量,为了控制惩罚项的大小。
求解模型参数
求解一组模型参数 $(w,b)$ 使得成本函数 $J$ 最小化。方法见梯度下降算法
$$ \arg \min_{w,b} J(w,b) $$
多项式回归
特征的多项式可提高模型复杂度,将其视作新特征则归来仍是线性回归问题。例子:以下式 $(1)(2)(3)$ 依次对应一元二次多项式、一元三次多项式、二元二次多项式模型:
$$ f_{w,b}(x) = w_1x + w_2x^2 + b \tag{1} $$
$$ f_{w,b}(x) = w_1x + w_2x^2 + w_3x^3 + b \tag{2} $$
$$ f_{w,b}(x) = w_1x_1 + w_2x_2 + w_3x_1x_2 + w_4x_1^2 + w_5x_2^2 + b \tag{3} $$
以式 $(1)$ 的模型为例,将将非一次项的 $x^2$ 视作新特征,即可按照线性回归模型训练。
逻辑回归
逻辑回归(Logistic Regression)是 Softmax 回归的特殊情况,都属于线性分类器。
问题背景
二分类(逻辑回归)
即二选一问题。将 $y|x \in \lbrace C_1,C_2 \rbrace$ 视为 $y$ 的条件概率下的伯努利分布,即:
- $p(y=1|x)$ 表示是 $C_1$ 的概率;
- $1 - p(y=1|x)$ 表示不是 $C_1$ 即是 $C_2$ 的概率;
因此仅需要找到一个概率分布函数:
$$ p(y=1|x) $$
然后取 $\displaystyle \max \lbrace p,1-p \rbrace$ 即以 $0.5$ 为分界,若 $p \geq 0.5$ 则分类为 $C_1$,否则分类为 $C_2$.
多分类(Softmax 回归)
即多选一问题。为 $y|x \in \lbrace C_1,C_2,\cdots,C_k \rbrace$ 找到 k 个 概率分布函数:
$$
\begin{cases}
p(y=1|x) \\
\\p(y=2|x) \\
\\ \cdots \\
\\p(y=k|x)
\end{cases}
$$
其中 $\displaystyle\sum_{i=1}^{k} p(y=i|x) = 1$,然后取 $\displaystyle \max_{i} p(y=i|x)$ 为最终分类类别。
逻辑回归
模型
逻辑回归假设 $y|x \sim Bernoulli(p)$,即 $y$ 的条件概率服从伯努利分布(0-1分布)。
$$ g(z) = \frac{1}{1+e^{-z}} \in (0,1) $$
令
$$ z = w \cdot x + b $$ 则 $y=1$(也称作正例)的概率模型:
$$
p(y=1|x;w,b) = g(z) = \frac{1}{1 + e^{-(w \cdot x + b)}}
$$
说明:
- 模型直接输出 $y=1$ 即正例的概率,即属于 $\mathbb{R}^n \to \mathbb{R}$ 单值函数;
- 如 $y^{(i)}$ 形如 $[0]$,$\hat{y}^{(i)}$ 形如 $[0.4]$.
以 0.5 为分界,若 $p \geq 0.5$ 则分类为 $1$,否则分类为 $0$. 因此别名对数逻辑回归;- 模型参数同线性回归。本质上是构造了一个线性决策边界 $z = w \cdot x + b = 0$;
成本函数
以下两种角度殊途同归。
极大似然估计角度
极大似然估计假设样本独立同分布,由模型 $p(y=1|x;w,b)$ 构造似然函数 $L(w,b)$:
$$
\begin{split}
L(w,b) &= \prod_{i:y^{(i)}=1} p(x^{(i)};w,b) \prod_{i:y^{(i)}=0} \left(1 - p(x^{(i)};w,b)\right) \\
\\&= \prod_{i=1}^{m} \left(p(x^{(i)};w,b)\right)^{y^{(i)}} \left(1 - p(x^{(i)};w,b)\right)^{1 - y^{(i)}}
\end{split}
$$
将目标由 $\displaystyle\arg \max_{w,b} L(w,b)$ 转化为取对数再取负号后求极小值问题,取均值后成本函数:
$$
J(w,b) = \frac{1}{m} \sum_{i=1}^{m} - y^{(i)} \ln p(x^{(i)};w,b) - (1 - y^{(i)}) \ln\left(1 - p(x^{(i)};w,b)\right)
$$
交叉熵损失角度
将真实类别 $y$ 和预测类别 $p(x;w,b)$ 看作分类类别的两个概率分布,则可使用交叉熵来衡量差异程度,即:
$$
\begin{split}
J(w,b) &= \frac{1}{m} \sum_{i=1}^{m} L(\hat{y}^{(i)}, y^{(i)}) = \frac{1}{m} \sum_{i=1}^{m} H(y^{(i)}, \hat{y}^{(i)}) \\
&= \frac{1}{m} \sum_{i=1}^{m} - y^{(i)} \ln p(x^{(i)};w,b) - (1 - y^{(i)}) \ln\left(1 - p(x^{(i)};w,b)\right)
\end{split}
$$
求解模型参数
求解一组模型参数 $(w,b)$ 使得成本函数 $J$ 最小化。方法见梯度下降算法
$$ \arg \min_{w,b} J(w,b) $$
Softmax 回归
模型
Softmax 解决多分类问题,设共 $k$ 个类别,对于每个类别,都对应一个线性映射:
$$ z_i = w_i \cdot x + b_i $$
则第 $i$ 个类别的概率模型:
$$
p(y=i|x;w_i,b_i) = g(z_i) = \frac{e^{z_i}}{\sum_{j=1}^{k} e^{z_j}}
$$
其中 $w_i \in \mathbb{R}^n, \space i \in \lbrace 1, 2, …, k \rbrace$,显然 $\displaystyle\sum_{i=1}^{k} p(y=i|x;w_i,b_i) = 1$.
说明:
- 模型直接输出 $k$ 个类别的概率,即属于 $\mathbb{R}^n \to \mathbb{R}^k$ 多值函数;
- 如 $k$ 取 3,则 $y^{(i)}$ 形如 $[0, 0, 1]$,$\hat{y}^{(i)}$ 形如 $[0.1, 0.4, 0.5]$.
- 最终分类类别取 $\displaystyle \max_i p(y=i|x)$ 对应的即可;
成本函数
使用交叉熵损失:
$$
\begin{split}
J &= \frac{1}{m} \sum_{i=1}^{m} L(\hat{y}^{(i)}, y^{(i)})
= \frac{1}{m} \sum_{i=1}^{m} H(y^{(i)}, \hat{y}^{(i)}) \\
\\&= \frac{1}{m} \sum_{i=1}^{m} \sum_{j=1}^{k} -y^{(i,j)} \ln p(x^{(i)};w_j,b_j)
\end{split}
$$
其中,$y^{(i,j)}$ 表示第 $i$ 个训练示例的第 $j$ 个分类的概率。
SVM
支持向量机,解决分类问题。
属于线性分类器。非线性问题,可通过 kernal SVM 解决(映射到高维);
超平面:
- 决策分界面(decision boundary)
- 边界分界面(margin boundary)
Hard-margin SVM
Soft-margin SVM:加入了容错率
核函数需满足:
$$ k(x,z) = g(x) g(z) $$
朴素贝叶斯
朴素贝叶斯(Naive Bayes),解决分类问题。
原理
朴素贝叶斯基于贝叶斯定理,并假设每个样本点的特征相互独立。
设 $x \in \mathbb{R}^n$,$y|x \in \lbrace C_1,C_2,\cdots,C_k \rbrace$,则给定待分类的 $x$,其属于 $C_i$ 类别的概率是:
$$
p(y=C_i|x) = \frac{p(y=C_i) p(x|y=C_i)}{p(x)} =
\frac{p(y=C_i) \prod_{j=1}^{n} p(x_j|y=C_i)}{\prod_{j=1}^{n} p(x_j)}
$$
然后取 $k$ 个类别中概率最大的作为预测类别,即:
$$
\arg \max_{C_i} p(y=C_i|x)
$$
说明:由于是比大小,因此可省去计算常量分母 $p(x)$,即:
$$
p(y=C_i|x)
\propto p(y=C_i) \prod_{j=1}^{n} p(x_j|y=C_i)
$$
拉普拉斯平滑
拉普拉斯平滑(Laplace smoothing)用于修正当 $p(x_j|y=C_i) = 0$ 时导致的连乘结果为零的零概率问题。方法是计算概率时分子+1
决策树
决策树(Decision tree)可解决分类和回归问题。核心思想是使用信息纯度的提升程度来衡量分类效率。
问题背景
特征:包含离散值和连续值;
标签:
决策树
设训练集有 $n$ 个类别特征,$k$ 个分类标签,则ID3算法的决策树基本原理如下:
步骤零
设置一个阈值 $\varepsilon$,当熵小于该值,则停止分类,因为此时信息纯度已足够高;
步骤一
计算分类前 $y$ 的熵:
$$ H(y) = - \sum_{i=1}^{k} p(y=i) \ln p(y=i) $$
说明:当 $H(y) < \varepsilon$ 时,没有分类的必要了。
步骤二
对于每个类别特征 $x_j$,计算其将 $y$ 分类后的熵:
$$ H(y|x_j), \space j \in \lbrace1,2,\cdots,n \rbrace$$
再计算分类前后的熵减即信息增益,选信息增益最大的那个特征作为分类特征:
$$ Gain(y,x_j) = H(y) - H(y|x_j) $$
说明:ID3算法使用信息增益,C4.5算法使用信息增益率。
步骤三
对于每个子类别节点,重复步骤一和步骤二(记得剔除已分类特征),直至所有的子类别节点都停止分类。
可选:连续特征离散化
回归树
对于回归树,使用方差衡量信息不纯度。其他类比决策树。
随机森林
随机森林(Random forest)是一种基于树模型的集成学习(Ensemble learning)方法。
思想:通过重复多次有放回抽样,且每次随机选择 $k<n$ 个特征,训练若干个权重相等的决策树(弱学习器),然后投票机制,分类问题则求众数,回归问题则求均值。
Bagging
XGBoost
也是一种集成学习方法,Boosting.
KNN
KNN (K-Nearest Neighbors),解决分类+回归问题。K 个邻居的意思。
原理
给定训练集 $X \in \mathbb{R}^{m \times n}, y \in \mathbb{R}^m$,则给定待分类的点(特征) $x$,其所属类别由距离其最近的 k 个点(邻居)决定。
$$
d(x, x^{(i)}) = \lVert x - x^{(i)} \rVert
= \sqrt{\sum_{j=1}^{n} (x_j - x_j^{(i)})^2}
$$
说明:非参数,投票制。回归问题,可取均值。
无监督学习
给定不包含标签的训练集 $X$,通过算法构建一个模型,揭示数据的内在分布特性及规律,即:$$ X \to f(x) \to \hat{y} $$
无监督学习任务分为聚类(Clustering)和降维(Dimensionality reduction)。
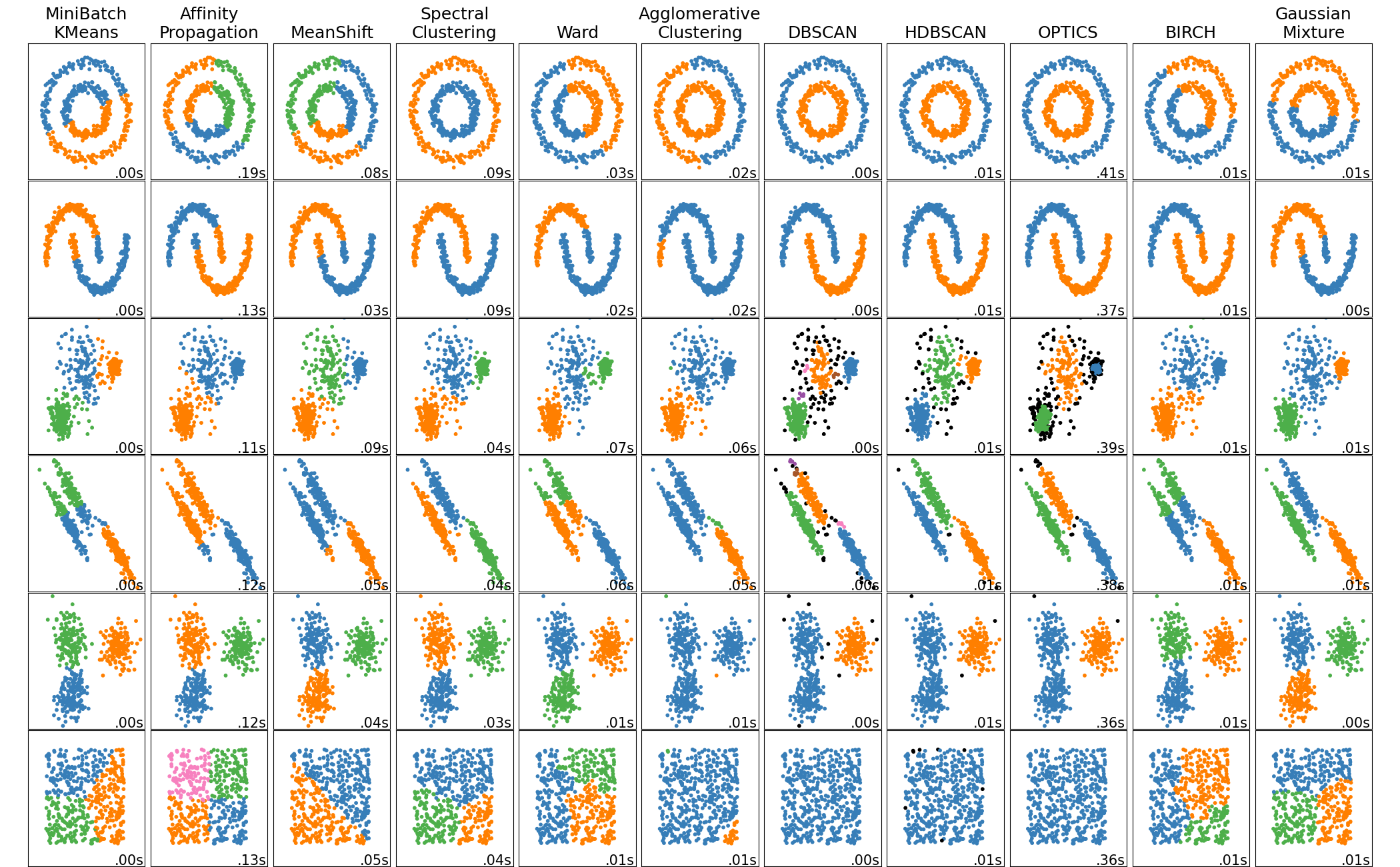
K-means
解决聚类问题。K 个类别的意思。
原理
给定训练集 $X \in \mathbb{R}^{m \times n}$,K-means 要实现的是将 $m$ 个点(训练示例)聚类为 $k$ 个簇(Cluster),步骤如下:
步骤一:随机初始化 $k$ 个簇中心,记作 $\mu_j \in \mathbb{R}^n$;
步骤二:为每个点 $x^{(i)}$ 分配距离最近的簇,记作 $c^{(i)}$:$$ c^{(i)} = \displaystyle\min_{j} \lVert x^{(i)} - \mu_j\rVert_2^2 $$
步骤三:为每个簇重新计算簇中心 $\mu_{j}$,方法是该簇中所有点的均值;
重复以上步骤二和步骤三,直至 $k$ 个簇中心不再发生变化(即收敛)。
成本函数可以表示为:
$$
J(c^{(1)}, \cdots, c^{(m)}, \mu_1, \cdots, \mu_k) = \frac{1}{m} \sum_{i=1}^{m} \lVert x^{(i)} - \mu_{c^{(i)}}\rVert_2^2
$$
其中:$\mu_{c^{(i)}}$ 表示 $x^{(i)}$ 所属的簇中心;
PCA
主成分分析(Principal Component Analysis, PCA),解决降维问题。
用最少的特征尽可能解释所有的方差(越离散方差越大)。
用途:特征工程,可视化。
机器学习基础
距离和相似度
对于向量 $x,y \in \mathbb{R}^n$,或空间中两个点,计算距离可使用差向量的大小的衡量如范数,计算相似度可通过两向量夹角等来衡量。
闵可夫斯基距离
是含参数 p 的距离函数。当 p 依次取 1, 2, $\infty$ 时,分别对应曼哈顿距离、欧氏距离、切比雪夫距离;
$$ \left(\sum_{j=1}^{n} {\lvert x_j - y_j \rvert}^p\right)^{1/p} \tag{$L_p$} $$
曼哈顿距离
$$ \sum_{j=1}^{n} \lvert x_j - y_j \rvert \tag{$L_1$} $$
欧氏距离
$$ \sqrt{\sum_{j=1}^{n} (x_j - y_j)^2} \tag{$L_2$} $$
切比雪夫距离
$$ \max_{j} {\lvert x_j - y_j \rvert} \tag{$L_{+\infty}$} $$
余弦相似度
使用两个向量夹角的余弦值来衡量相似度,公式如下:
$$ Cosine \space Similarity = \cos(\theta) = \frac{x \cdot y}{\lVert x \rVert \lVert y \rVert} $$
说明:由向量点积计算公式推导而来。越接近于 1,夹角越接近于 0,越相似。
皮尔逊相关系数
使用标准化后的协方差来衡量两个随机变量的线性相关性。
$$
\rho = \frac{Cov(X,Y)}{\sigma_X \sigma_Y} \in [-1, 1]
$$
说明:越接近于 1 越正线性相关,越接近于 -1 越负线性相关,等于 0 不线性相关。
KL 散度
给定两个概率分布 $p(x)$ 和 $q(x)$,使用 KL 散度来衡量两者之间的差异程度,公式如下:
$$ D_{KL}(p||q) = \sum_x p(x) \ln \frac{p(x)}{q(x)} \in [0, \infty] $$
说明:也称作相对熵。非负,越小越相似。
特征工程
EDA
探索阶段,包括:
- 缺失值;
- 异常值;(PCA 后可视化)
- 线性相关性;
| |
缺失值处理
离散值
删除:缺失比例严重时;取众数;逻辑回归:使用完整数据预测缺失数据;不处理:算法不敏感时,如 XGBoost;
连续值
删除:缺失比例严重时;取中位数:(相对均值更能兼容偏态分布)线性回归:使用完整数据预测缺失数据;不处理:算法不敏感时,如 XGBoost;
异常值处理
如何发现:
LabelEncoder
主要用于将离散特征的多个(有序)类别,映射为有序数字。例子:
| 原特征 | 新特征 |
|---|---|
| $C_1$ | 0 |
| $C_2$ | 1 |
| $C_3$ | 2 |
One-Hot 编码
主要用于将离散特征的多个(无序)类别,转为稀疏矩阵。例子:
| 原特征 | 新特征1 | 新特征2 | 新特征3 |
|---|---|---|---|
| $C_1$ | 1 | 0 | 0 |
| $C_2$ | 0 | 1 | 0 |
| $C_3$ | 0 | 0 | 1 |
分箱
主要用于连续特征的离散化。例子:
| 原特征 | 新特征 |
|---|---|
| $[0, 60)$ | 0 |
| $[60,80)$ | 1 |
| $[80,100]$ | 2 |
特征缩放
特征缩放(Feature scaling)主要通过归一化(Normalization)和标准化(Standardization)实现。主要目的是:
- 剔除量纲,解决
数据可比性问题; - 提高求解速度,如运行梯度下降时更快收敛。
最大最小归一化
Min-max normalization (Rescaling):
$$
x^{\prime} = \frac{x - min(x)}{max(x) - min(x)}
$$
说明:归一化后取值范围为 $[0,1]$,适用于最大最小值较稳定的情况;
均值归一化
Mean normalization:
$$
x^{\prime} = \frac{x - \bar{x}}{max(x) - min(x)}
$$
说明:归一化后取值范围为 $[-1,1]$;
Z 分数归一化
Z-score normalization,也称作标准化(Standardization):
$$
x^{\prime} = \frac{x - \mu}{\sigma}
$$
说明:归一化后取值范围为 $[-\infty,+\infty]$,且均值为 $0$,标准差为 $1$;
特征提取
如从文本、图像中提取机器学习可支持的特征。
| |
特征选择
去除变化小(方差小)的特征:
去除共线(线性相关)的特征:
损失函数
衡量单个预测值与真实值之间的差异程度。损失函数通常表示为 $L(\hat{y}, y)$,成本函数通常表示为 $J = \frac{1}{m} \displaystyle \sum_{i=1}^{m} L\left(\hat{y}^{(i)}, y^{(i)}\right)$.
最小二乘
适用于回归模型。给定 $\hat{y},y \in \mathbb{R}$,分别表示预测值和真实值,则:
$$ L(\hat{y}, y) = \frac{1}{2} (\hat{y} - y)^2 $$
交叉熵
适用于分类模型。将 $\hat{y},y$ 分别看作 预测类别的分布和真实类别的分布,则:
$$ L(\hat{y}, y) = H(y,\hat{y}) = - \sum_k y \ln \hat{y} $$
其中 $k$ 为分类的数量,$\displaystyle\sum_{k} y = \sum_{k} \hat{y} = 1$. 推导详见交叉熵。
特别的,对于二分类问题:
$$ L(\hat{y}, y) = -y\ln\hat{y} - (1-y)\ln(1-\hat{y}) $$
举例说明:
对于二分类,$\hat{y},y$ 的一组取值形如 $[0.6]$ 和 $[1]$,本质上是 $[0.6, 0.4]$ 和 $[1, 0]$;
对于三分类问题,$\hat{y},y$ 的一组取值形如 $[0.1, 0.3, 0.6]$ 和 $[0, 0, 1]$;
优化算法
梯度下降算法
在某点沿着梯度反方向,函数值下降最快。梯度下降(Gradient Descent, GD)是一种迭代优化算法,用于求解任意一个可微函数的局部最小值。在机器学习中,常用于最小化成本函数,即:
给定成本函数 $J(w,b)$,求解一组 $(w,b)$,使得
$$ arg\min_{w,b} J(w,b) $$
实现方法
步骤一:选定初始点 $(w_{init},b_{init})$;
步骤二:为了使函数值下降,需要沿着梯度反方向迭代,即重复以下步骤,直至收敛,即可得到局部最小值的解:
$$
w \leftarrow w - \alpha \frac{\partial J}{\partial w}
$$
$$
b \leftarrow b - \alpha \frac{\partial J}{\partial b}
$$
即:
$$
\begin{equation}
\begin{pmatrix}
w_1 \\
w_2 \\
\vdots \\
w_n \\
b
\end{pmatrix}
\leftarrow
\begin{pmatrix}
w_1 \\
w_2 \\
\vdots \\
w_n \\
b
\end{pmatrix}
- \alpha
\begin{pmatrix}
\frac{\partial J}{\partial w_1} \\
\frac{\partial J}{\partial w_2} \\
\vdots \\
\frac{\partial J}{\partial w_n} \\
\frac{\partial J}{\partial b}
\end{pmatrix}
\end{equation}
$$
其中:$\alpha \geq 0$ 指学习率(Learning rate),也称作步长,决定了迭代的次数。
批量梯度下降
(Batch Gradient Descent, BGD):使用训练集中的所有数据
随机梯度下降
(stotastic gradient descent, SGD):??根据每个训练样本进行参数更新
模型评估
过拟合问题
定义过拟合:训练方差小,测试方差大。
解决过拟合的方法:
- 收集更多的训练示例;
- 特征选择;
- 正则化;
评估方法
留出法(Hold-out):拆分训练集和测试集,如经验上 8/2 或 7/3;
交叉验证法(Cross Validation):将数据集分成 N 块,使用 N-1 块进行训练,再用最后一块进行测试;
自助法(Bootstrap):有放回随机抽样;
回归指标
MAE
MAE(Mean Absolute Error),平均绝对误差。
$$ MAE = \frac{1}{m} \sum_{i=1}^{m} \lvert \hat{y}^{(i)} - y^{(i)} \rvert $$
MAPE
MAPE(Mean Absolute Percentage Error),平均绝对百分误差。
$$ MAPE = \frac{100}{m} \sum_{i=1}^{m} \lvert \frac{y^{(i)} - \hat{y}^{(i)}}{y^{(i)}} \rvert $$
MSE
MSE(Mean Squared Error),均方误差。最小二乘的均值版,常用于回归模型。
$$ MSE = \frac{1}{m} \sum_{i=1}^{m} (\hat{y}^{(i)} - y^{(i)})^2 $$
RMSE
RMSE(Root Mean Square Error),均方根误差。
$$ RMSE = \sqrt{MSE} $$
R2
R2 (coefficient of determination),决定系数。衡量总误差(客观存在且无关回归模型)中可以被回归模型解释的比例,即拟合程度。
$$ R^2 = \frac{SSR}{SST} = 1- \frac{SSE}{SST} $$
说明:
当 $R^2 \to 1$ 时,表明拟合程度越好,因为此时 SSR 趋向于 SST(或 SSE 趋向于 0);
当 $R^2 \to 0$ 时,表明拟合程度越差,因为此时 SSR 趋向于 0(或 SSE 趋向于 SST);
分类指标
二分类问题的混淆矩阵(Confusion Matrix)如下:
| actual/predicted | Positive | Negative |
|---|---|---|
| Positive | TP(真阳) | FN(假阴) |
| Negative | FP(假阳) | TN(真阴) |
其中:T/F 表示预测是否正确,P/N 表示预测结果(P=1, N=0)。
准确率
指预测正确的比例,即:
$$ accuracy = \frac{TP+TN}{TP+TN+FP+FN} $$
精确率
也称作查准率,指预测为正的样本中,实际也为正的比例,即:
$$ precision = \frac{True \space P}{predicted \space P} = \frac{TP}{TP+FP} $$
召回率
也称作查全率,指实际为正的样本中,判定也为正的比例,即:
$$ recall = \frac{True \space P}{actual \space P} = \frac{TP}{TP+FN} $$
F1
$$ F1 = \frac{2 \times precision \times recall}{precision + recall} $$
ROC 曲线
指以 FPR 为横轴, TPR 为纵轴绘制成的曲线。其中:
FPR 指假阳率,也称作误诊率,指实际为阴,但判定为阳的比例,即:
$$ FPR = \frac{FP}{FP+TN} $$
TPR 指真阳率,就是召回率,指实际为阳,判断也为阳的比例,即:
$$ TPR = \frac{TP}{TP+FN} $$
说明:FPR 越低,TPR 越高,也就是越靠近 (0, 1),说明模型分类能力越好。
AUC
AUC (Area Under ROC Curve)指的是 ROC 曲线下方的面积,相较于 ROC,是一个直观的标量来衡量模型分类能力。
- $AUC=1$: 即左上角,完美分类;
- $AUC=0.5$: 即分类能力与随机的抛硬币毫无差异,比较差;
- $AUC<0.5$: 分类能力很差,反着来;
实际中,一般在 $0.5 \to 1$ 之间。
PR 曲线
指以 Recall 为横轴, precision 为纵轴绘制成的曲线。
数学基础
矩
设随机变量 $X$ 和 $Y$,正整数 $k$ 和 $l$.
原点矩
原点指坐标原点。$X$ 的 $k$ 阶原点矩:
$$ E(X^k) $$
中心矩
中心指期望值。$X$ 的 $k$ 阶中心矩记作 $\mu_k$:
$$ \mu_k = E\lbrack X - E(X)\rbrack^k $$
标准矩
标准化指除以标准差以剔除量纲,标准矩是标准化的中心矩。$X$ 的 $k$ 阶标准矩:
$$
\frac{\mu_k}{\sigma^k} = \frac{\mu_k}{\mu_2^{\frac{k}{2}}} = \frac{E\lbrack X - E(X)\rbrack^k}{\left(E\lbrack X - E(X)\rbrack^2\right)^{\frac{k}{2}}}
$$
混合矩
$X$ 和 $Y$ 的 $k+l$ 阶混合矩:
$$ E(X^kY^l) $$
混合中心矩
$X$ 和 $Y$ 的 $k+l$ 阶混合中心矩:
$$ E\lbrace\lbrack X - E(X)\rbrack^k \lbrack Y - E(Y)\rbrack^l \rbrace $$
统计指标
注意这里不严格区分总体和样本,并使用样本估计整体。
极差
$$ \max(x) - \min(x) $$
期望值
这里使用样本均值估计总体期望值。
$$
\begin{split}
\mu &= E(X) = \sum_{j=1}^{N} p(x_j) x_j \\
&\approx \bar{x} = \frac{1}{n} \sum_{j=1}^{n} x_j
\end{split}
$$
样本均值依概率 1 收敛于期望值。期望值与均值
总体期望值是常数标量,样本均值依赖于具体的随机抽样。
如抛硬币(伯努利试验),总体期望值是 $0.5 * 1 + 0.5 * 0 = 0.5$,但样本均值比如抛 3 次 $(1+1+0)/3 \neq 0.5$.
方差
方差(Variance)用于衡量相对均值的离散程度。
$$
\begin{split}
\sigma^2 &= Var(X) = E\lbrack X - E(X)\rbrack^2 = \sum_{j=1}^{N} p(x_j)(x_j - \mu)^2 \\
&\approx \frac{1}{n} \sum_{j=1}^{n} (x_j - \bar{x})^2
\end{split}
$$
说明:越大,越扁,越离散,熵越大。
标准差
标准差(Standard deviation)是方差的正平方根。
$$ \sigma = \sqrt{\sigma^2} $$
协方差
协方差(Covariance)用于衡量两个变量的线性相关性。
$$
Cov(X,Y) = E\lbrace\lbrack X - E(X)\rbrack \lbrack Y - E(Y)\rbrack \rbrace
$$
说明:$Cov(X,X) = Var(X)$,即方差是协方差的特殊情形。
相关系数
标准化的协方差。
$$
\rho = \frac{Cov(X,Y)}{\sigma_X \sigma_Y}
$$
偏度
偏度(Skewness)用于衡量分布的对称性。
$$
Skewness = \frac{\mu_3}{\sigma^3} = \frac{\mu_3}{\mu_2^{\frac{3}{2}}}
$$
说明:尾巴在哪边就偏哪边。
峰度
峰度(Kurtosis)用于衡量相对高斯分布的陡峭程度。
$$
Kurtosis = \frac{\mu_4}{\sigma^4} - 3 = \frac{\mu_4}{\mu_2^2} - 3
$$
说明:减常数 3 是为了使高斯分布的峰度为零。
导数
给定函数 $f: \mathbb{R} \to \mathbb{R}$,则 $f$ 在点 $x$ 处的一阶导数 $f'$ 和二阶导数 $f''$ 的定义分别如下:
$$
f' = \frac{dy}{dx} = \lim_{{\Delta x} \to 0} \frac{f(x + {\Delta x})}{\Delta x}
$$
$$ f'' = (f')' = \frac{d^2y}{dx^2} $$
注意:可导等于可微,可导一定连续;
说明:一阶导表示函数在该点处的瞬时变化率;
用途:一阶导用于判断单调性;二阶导用于判断凹凸性,大于零则凸(U 型)。
偏导数
给定函数 $f: \mathbb{R}^n \to \mathbb{R}$,则 $f$ 对自变量 $x_j$ 的偏导数(partial derivative),指将其他自变量视作常量时,对 $x_j$ 的导数,即:
$$
\frac{\partial f}{\partial x_j} = \lim_{{\Delta x_j} \to 0} \frac{f(x_j + {\Delta x_j}, …) - f(x_j, …)}{\Delta x_j}
$$
注意:可微一定可导,可微一定连续。
梯度
给定可微函数 $f: \mathbb{R}^n \to \mathbb{R}$,则 $f$ 的偏导数构成的向量,称为梯度,记作 $grad f$ 或 $\nabla f$,即:
$$
grad f = \nabla f =
\begin{bmatrix}
\frac{\partial f}{\partial x_1} \\
\frac{\partial f}{\partial x_2} \\
\vdots \\
\frac{\partial f}{\partial x_n}
\end{bmatrix} \in \mathbb{R}^n
$$
用途:梯度下降算法
凸函数
如果一个函数满足任意两点连成的线段都位于函数图形的上方,则称这个函数为凸函数(Convex function)。
凸函数的局部最小值等于极小值,可作为选择损失函数的重要参考。
向量
n 维向量 $x$ 记作:
$$
x = \begin{bmatrix}x_1 \\ x_2 \\ \vdots \\ x_n \end{bmatrix} \in \mathbb{R}^n
$$
说明:本文一律默认列向量,在 Python 中对应一维数组。$x$ 也可视作一个 $n \times 1$ 矩阵。
数乘
几何意义是向量的伸缩 (stretch)。
加法
几何意义是向量的旋转 (rotate)。
点积
点积(Dot product),也称作点乘、内积、数量积。对于 $x,y \in \mathbb{R}^n$:
$$
x \cdot y = x^Ty = \sum_{j=1}^{n} x_jy_j \in \mathbb{R}
$$
注意:相同维数才能进行点积乘法;
说明:几何意义是向量围成的平面的面积或空间的体积(有正负号),大小等于 $\lVert x \rVert \lVert y \rVert\cos(\theta)$,其中 $\theta$ 为两向量之间的夹角;
用途:余弦相似度
叉积
叉积(Cross product),也称作叉乘、向量积。对于 $x,y \in \mathbb{R}^3$:
$$
\begin{split}
x \times y &=
\left|
\begin{matrix}
\vec{i} & \vec{j} & \vec{k} \\
x_1 & x_2 & x_3 \\
y_1 & y_2 & y_3
\end{matrix}
\right| \\
\\&= (x_2y_3-x_3y_2)\vec{i} - (x_1y_3-x_3y_1)\vec{j} + (x_1y_2-x_2y_1)\vec{k} \\
\\&= \begin{bmatrix}x_2y_3-x_3y_2 \\ -(x_1y_3-x_3y_1) \\ x_1y_2-x_2y_1 \end{bmatrix} \in \mathbb{R}^3
\end{split}
$$
注意:叉积的概念仅用于三维空间。这里的公式表达使用了行列式和代数余子式;
说明:几何意义是法向量,大小等于 $\lVert x \rVert \lVert y \rVert \sin(\theta)$,其中 $\theta$ 为两向量之间的夹角。
外积
外积(Outer product)。对于 $x \in \mathbb{R}^m, y \in \mathbb{R}^n$:
$$
x \otimes y = xy^T =
\begin{bmatrix}
x_1y_1 & x_1y_2 & \dots & x_1y_n \\
x_2y_1 & x_2y_2 & \dots & x_2y_n \\
\vdots & \vdots & \ddots & \vdots \\
x_my_1 & x_my_2 & \dots & x_my_n
\end{bmatrix}
\in \mathbb{R}^{m \times n}
$$
说明:运算结果是个矩阵。
矩阵
$m \times n$ 矩阵可理解为 n 个列向量的集合(或 m 个行向量的集合)。
线性组合
各自数乘再相加,结果仍是同维向量。设有 n 个 m 维向量 $x_1,x_2,…,x_n$ 和 n 个标量 $w_1,w_2,…,w_n$,则该 n 个向量的线性组合 $y$ 表示如下:
$$ y = w_1x_1 + w_2x_2 + \cdots + w_nx_n \in \mathbb{R}^m $$
说明:线性空间内,数乘运算本质上是向量的伸缩,加法运算本质上是向量的旋转。线性运算并没有对向量进行扭曲和变形。
线性相关
对于 n 个向量 $x_1,x_2,…,x_n$,令其线性组合为零向量,即:
$$ w_1x_1 + w_2x_2 + \cdots + w_nx_n = \vec{0} $$
如果当且仅当 $w_1 = w_2 = \cdots = w_n = 0$ 即全部系数为零时才成立,则称该 n 个向量线性无关,否则线性相关。
说明:线性相关,则其中一个可以用其余的线性组合表示,此时可降维。
秩
矩阵的秩(Rank)记作 $rank$,且秩 = 列秩 = 行秩。
对于 $X \in \mathbb{R}^{m \times n}$,由于实际中 $m \gg n$,因此其秩由 $n$ 决定。且:
- 若 $rank(X) = n$,即列满秩,则 n 个特征线性无关;
- 若 $rank(X) < n$,即列不满秩,则 n 个特征线性相关,此时可降维。
行列式
行列式(Determinant)针对的是方阵。对于方阵 $X \in \mathbb{R}^{n \times n}$,其行列式记作 $\det(X)$,且:
若满秩则 $det(X) \neq 0$,称为非奇异矩阵;
若不满秩则 $det(X) = 0$,称为奇异矩阵;
说明:奇异矩阵无法求逆矩阵。
线性变换
回忆线性组合,可将其写为矩阵乘向量即 $Xw=y$ 的形式:
$$
\begin{split}
\begin{bmatrix}x_{11} & x_{12} & \cdots & x_{1n} \\ x_{21} & x_{22} & \cdots & x_{2n} \\ \vdots & \vdots & \ddots &\vdots \\ x_{m1} & x_{m2} & \cdots & x_{mn} \end{bmatrix}
\begin{bmatrix}w_1 \\ w_2 \\ \vdots \\ w_n \end{bmatrix}
&= \begin{bmatrix}y_1 \\ y_2 \\ \vdots \\ y_m \end{bmatrix}
\end{split}
$$
理解上述式子:
- 代数角度:n 个列向量的
线性组合; - 几何角度:对 n 个列向量
先各自缩放再旋转; - 线性变换的几何角度:将向量 $w$
线性变换至 $y$,具体指:- 输入向量:$w$
- 线性变换:$X$,其中 n 个列向量可视作伪基向量;
- 输出向量:$y$
矩阵乘向量
对向量进行一次线性变换。例子:
$$
\begin{bmatrix}a & b & c \\ d & e & f \\ g & h & i \end{bmatrix}
\begin{bmatrix}x \\ y \\ z \end{bmatrix} =
x \begin{bmatrix}a \\ d \\ g \end{bmatrix} +
y \begin{bmatrix}b \\ e \\ h \end{bmatrix} +
z \begin{bmatrix}c \\ f \\ i \end{bmatrix} =
\begin{bmatrix}ax+by+cz \\ dx+ey+fz \\ gx+hy+iz \end{bmatrix}
$$
特别的,当取正交单位矩阵时,该向量经过线性变化后,仍等于该向量。
$$
\begin{bmatrix}1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{bmatrix}
\begin{bmatrix}x \\ y \\ z \end{bmatrix} =
x \begin{bmatrix}1 \\ 0 \\ 0 \end{bmatrix} +
y \begin{bmatrix}0 \\ 1 \\ 0 \end{bmatrix} +
z \begin{bmatrix}0 \\ 0 \\ 1 \end{bmatrix} =
\begin{bmatrix}x \\ y \\ z \end{bmatrix}
$$
矩阵乘矩阵
两次线性变换的叠加(自右向左)。例子:
特征值与特征向量
给定方阵 $A \in \mathbb{R}^{n \times n}$,若存在非零向量 $v \in \mathbb{R}^n$ 和非零标量 $\lambda \in \mathbb{R}$,使得:
$$
Av = \lambda v
$$
则称 $v$ 为方阵 $A$ 的特征向量,$\lambda$ 为对应的特征值。
理解:$v$ 在 $A$ 线性变换的作用下,仅发生了数乘 $\lambda v$,几何意义上即仅发生了缩放。
特征分解
三次线性变换的叠加。自右向左,先旋转,再伸缩,最后再旋转。特征分解是一种矩阵分解,且针对的是方阵。给定方阵 $A \in \mathbb{R}^{n \times n}$,则可将其分解为三个矩阵相乘:
$$
A = V diag(\lambda) V^{-1}
$$
其中:
- $V \in \mathbb{R}^{n \times n}$:指 $A$ 的 n 个特征向量组成的
正交矩阵; - $diag(\lambda) \in \mathbb{R}^{n \times n}$:指对应 n 个特征值在对角线上的
对角矩阵; - $V^{-1}$:指 $V$ 的逆矩阵;
例子(以下四个矩阵依次对应 $A, V, diag(\lambda), V^{-1}$):
$$
\begin{bmatrix}1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 0 \end{bmatrix} =
\begin{bmatrix}0 & 1 & 0 \\ 1 & 0 & 0 \\ 0 & 0 & 1 \end{bmatrix}
\begin{bmatrix}1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 0 \end{bmatrix}
\begin{bmatrix}0 & 1 & 0 \\ 1 & 0 & 0 \\ 0 & 0 & 1 \end{bmatrix}
$$
理解:向量 $\begin{bmatrix}1 & 1 & 0 \end{bmatrix}^T$ 和 $\begin{bmatrix}1 & 1 \end{bmatrix}^T$ 本质上一个属于三维,一个属于二维。
奇异值分解
给定矩阵 $A \in \mathbb{R}^{m \times n}$,则可将其分解为三个矩阵相乘:
$$
A = U \Sigma V^T
$$
其中:
- $U \in \mathbb{R}^{m \times m}$:指 $AA^T$ 的 m 个特征向量组成的
左正交矩阵; - $\Sigma \in \mathbb{R}^{m \times n}$:指
对角阵,对角线上的 $\sigma$ 称为奇异值,非负且降序排列,可理解为特征的权重;- 形如 $\begin{bmatrix}\sigma_1 & 0 \\ 0 & \sigma_2 \\ 0 & 0 \end{bmatrix}$ 时,起到
降维的作用; - 形如 $\begin{bmatrix}\sigma_1 & 0 & 0 \\ 0 & \sigma_2 & 0 \end{bmatrix}$ 时,起到
升维的作用;
- 形如 $\begin{bmatrix}\sigma_1 & 0 \\ 0 & \sigma_2 \\ 0 & 0 \end{bmatrix}$ 时,起到
- $V^T \in \mathbb{R}^{n \times n}$:指 $A^TA$ 的 n 个特征向量组成的
右正交矩阵;
降维的原理,即取前 k 个权重高的特征来近似表示整个矩阵:
$$
A_{m \times n} =
U_{m \times m} \Sigma_{m \times n} V_{n \times n}^T \approx
U_{m \times k} \Sigma_{k \times k} V_{k \times n}^T
$$
降维例子(以下四个矩阵依次对应 $A, U, \Sigma, V^T$):
$$
\begin{split}
\begin{bmatrix}1 & 2 \\ 3 & 4 \\ 5 & 6 \end{bmatrix} &=
\begin{bmatrix}-0.2298477 & 0.88346102 & 0.40824829 \\ -0.52474482 & 0.24078249 & -0.81649658 \\ -0.81964194 & -0.40189603 & 0.40824829 \end{bmatrix}
\begin{bmatrix}9.52551809 & 0 \\ 0 & 0.51430058 \\ 0 & 0 \end{bmatrix}
\begin{bmatrix}-0.61962948 & -0.78489445 \\ -0.78489445 & 0.61962948 \end{bmatrix} \\
\\ &\approx
\begin{bmatrix}-0.2298477 & 0.88346102 \\ -0.52474482 & 0.24078249 \\ -0.81964194 & -0.40189603 \end{bmatrix}
\begin{bmatrix}9.52551809 & 0 \\ 0 & 0.51430058 \end{bmatrix}
\begin{bmatrix}-0.61962948 & -0.78489445 \\ -0.78489445 & 0.61962948 \end{bmatrix}
\end{split}
$$
范数
向量范数
n 维向量 $x$ 的 p 范数定义如下:
$$
L_p(x) = \lVert x \rVert_p = \left(\sum_{j=1}^{n} {\lvert x_j \rvert}^p\right)^{1/p}
$$
则当 p 依次取 $-\infty, 1, 2, +\infty$ 时,分别对应如下范数:
$$
\lVert x \rVert_{-\infty} = \lim_{p \to -\infty} \left(\sum_{j=1}^{n} {\lvert x_j \rvert}^p\right)^{1/p} =
\min_{j} {\lvert x_j \rvert} \tag{$L_{-\infty}$}
$$
$$
\lVert x \rVert_1 = \sum_{j=1}^{n} {\lvert x_j \rvert} \tag{$L_1$}
$$
$$
\lVert x \rVert_2 = \left(\sum_{j=1}^{n} {\lvert x_j \rvert}^2\right)^{1/2} \tag{$L_2$}
$$
$$
\lVert x \rVert_{+\infty} = \lim_{p \to +\infty} \left(\sum_{j=1}^{n} {\lvert x_j \rvert}^p\right)^{1/p} =
\max_{j} {\lvert x_j \rvert} \tag{$L_{+\infty}$}
$$
补充说明:
矩阵范数
极大似然估计
已知样本数据估计(反推)概率分布参数的方法。极大似然估计(Maximum Likelihood Estimation)的思想是,假设 m 个样本独立同分布于目标概率分布函数 $p(x;\theta)$,然后构造一个似然函数 $L(\theta)$ 来表示 m 个样本的联合概率,通过最大化这个联合概率来求解参数 $\theta$,即:
$$ L(\theta) = p(x^{(1)}, x^{(2)}, \cdots, x^{(m)}) = \prod_{i=1}^{m} p(x^{(i)};\theta) $$
其中 $\lbrace x^{(1)}, x^{(2)}, \cdots, x^{(m)} \rbrace$ 为已知样本数据。
说明:由于假设样本独立同分布,则联合概率等于各自概率的乘积。
贝叶斯定理
贝叶斯定理(Bayes’theorem)公式如下(其中 $P(B) \neq 0$):
$$ P(A|B) = \frac{P(B|A)P(A)}{P(B)} $$
说明:
- 可由条件概率 $P(A,B) = P(A|B)P(B) = P(B|A)P(A)$ 推导得到;
- $P(A|B)$ 是 $A$ 的后验概率,$P(A)$ 是 $A$ 的先验概率,$\frac{P(B|A)}{P(B)}$ 称作标准似然度,因此贝叶斯公式可表示为:$$ A 的后验概率 = A 的先验概率 * 标准似然度 $$
基础知识背景见下方。
联合概率
$A$ 和 $B$ 同时发生的概率,记作 $P(A,B)$ 或 $P(AB)$ 或 $P(A \cap B)$.
条件概率
$B$ 发生的条件下 $A$ 发生的概率,记作 $A$ 的条件概率 $P(A|B)$,其中 $P(B) \neq 0$:$$ P(A|B) = \frac{P(A,B)}{P(B)} $$
先验概率
以经验进行判断,如 $P(A)$.
后验概率
以结果进行判断。当条件概率 $P(A|B)$ 中隐含 $A$(因)会导致 $B$(果)发生时,则称此条件概率为 $A$ 的后验概率,可理解为 $P(因|果)$。
相互独立
$A$ 与 $B$ 相互独立,当且仅当以下成立:
$$P(A,B) = P(A)P(B)$$
概率分布函数
离散型随机变量对应概率质量函数(Probability Mass Function, PMF),连续型随机变量对应概率密度函数(Probability Density Function, PDF)。
均匀分布
随机变量 $X = \lbrace a_1,a_2,\cdots,a_n \rbrace$ 服从均匀分布,则:
$$ p(X=x) = \frac{1}{n} \tag{PMF} $$
随机变量 $X \in [a,b]$ 服从均匀分布,则:
$$
p(X=x) =
\begin{cases}
\frac{1}{b-a} & \text{if $x \in [a,b]$} \\
\\0 & \text{if $x \notin [a,b]$}
\end{cases} \tag{PDF}
$$
伯努利分布
指每次试验的结果只有两种可能,要么成功(1),要么失败(0)。设成功(1)的概率为 $p$,则成功(1)发生的次数 $X$ 服从伯努利分布,记作:
$$
X \sim Bernoulli(p)
$$
其中 $x \in \lbrace 0, 1 \rbrace$,有:
$$
p(X=x;p) = p^x(1-p)^{1-x} \tag{PMF}
$$
$$ \mu = p $$
$$ \sigma^2 = p(1-p) $$
说明:上述试验称为伯努利试验。
二项分布
指每次试验的结果只有两种可能,重复 n 次试验,设成功(1)的概率为 $p$,则成功(1)发生的次数 $X$ 服从二项分布,记作:
$$
X \sim B(n, p)
$$
其中 $x \in \lbrace 0, 1, …, n \rbrace$,有:
$$
p(X=x;n,p) = \frac{n!}{x!(n-x)!} p^x (1-p)^{n-x} \tag{PMF}
$$
$$ \mu = np $$
$$ \sigma^2 = np(1-p) $$
多项分布
指每次试验的结果有 k 种可能,重复 n 次试验,设结果 $j$ 的概率为 $p_j$,则所有结果发生的次数 $X = (X_1, \cdots, X_k)$ 服从多项分布,记作:
$$
X \sim M(n, p_1, \cdots, p_k)
$$
其中 $x_j \in \lbrace 0,\cdots n \rbrace, \sum_{j=1}^k x_j = n$,有:
$$
p(X_1=x_1,\cdots,X_k=x_k;n,p_1,\cdots,p_k) = \frac{n!}{x_1! \cdots x_k!} p_1^{x_1} \cdots p_k^{x_k} \tag{PMF}
$$
说明:
- 当 $k=2,n=1$ 时对应伯努利分布;
- 当 $k=2,n>1$ 时对应二项分布;
- 当 $k>2,n>1$ 时对应多项分布。
泊松分布
指单位时间内,若随机事件发生的次数的期望值为 $\lambda$,则随机事件发生的次数 $X$ 服从泊松分布,记作:
$$
X \sim Poisson(\lambda)
$$
其中 $x \in \lbrace 0, 1, \cdots \rbrace$,有:
$$
p(X=x;\lambda) = \frac{\lambda^x}{x!} e^{- \lambda} \tag{PMF}
$$
$$ \mu = \lambda $$
$$ \sigma^2 = \lambda $$
高斯分布
随机变量 $X$ 服从均值 $\mu$,方差 $\sigma^2$ 的高斯(正态)分布,记作:
$$
X \sim N(\mu, \sigma^2)
$$
其中 $x \in [-\infty, +\infty]$,有:
$$
p(X=x;\mu,\sigma) = \frac{1}{\sigma \sqrt{2 \pi}} \exp\left(-\frac{(x-\mu)^2} {2 \sigma^2}\right) \tag{PDF}
$$
说明:方差越大,分布越分散(混乱),越扁,熵越大(平均信息量越大)。
指数分布
指单位时间内,若随机事件发生的次数的期望值为 $\lambda$,则随机事件发生的时间间隔 $X$ 服从指数分布,记作:
$$
X \sim \exp(\lambda)
$$
其中 $x \in [0, +\infty]$,有:
$$
p(X=x;\lambda) = \lambda e^{-\lambda x} \tag{PDF}
$$
$$ \mu = \frac{1}{\lambda} $$
$$ \sigma^2 = \frac{1}{\lambda^2} $$
熵
信息量
给定随机变量 $X$ 的概率分布 $p(x) \in [0,1]$,则当 $X=x$ 发生时,$x$ 的信息量定义如下:
$$ I(x) = \ln \frac{1}{p(x)} = - \ln p(x) $$
其中 $\displaystyle \sum_x p(x) = 1$.
说明:
- 信息量针对的是
单一事件,大小仅受概率影响。概率越小,信息量越大; - 对数底数仅影响量化的单位,以 2 为底对应比特,以 e 为底对应纳特(默认)。
熵
熵(Entropy)等于随机变量 $X$ 所有可能取值的 信息量的期望值,用于衡量混乱程度或不确定性,定义如下:
$$
H(X) = E(I(x)) = \sum_x p(x) I(x) = - \sum_x p(x) \ln p(x)
$$
说明:
- 熵针对的是
整个概率分布,也记作 $H(p)$。熵越大(平均信息量越大),分布越混乱; - 离散型随机变量对应求和,连续型随机变量对应求积分(已省略);
相对熵
相对熵(Relative Entropy),又称为 KL 散度(Kullback-Leibler divergence),用于衡量两个概率分布之间的差异程度。对于随机变量 $X$ 的两个概率分布 $p(x)$ 和 $q(x)$,其相对熵定义如下:
$$ D_{KL}(p||q) = \sum_x p(x) \ln \frac{p(x)}{q(x)} $$
说明:非负,且越小,则 $p(x)$ 和 $q(x)$ 分布越接近;
交叉熵
将上述相对熵公式展开:
$$
\begin{split}
D_{KL}(p||q) &= \sum_x p(x) \ln \frac{p(x)}{q(x)} \\
\\&= \sum_x p(x) \ln p(x) - \sum_x p(x) \ln q(x) \\
\\&= -H(p) + H(p,q)
\end{split}
$$
其中,前半部分就是负的 $p(x)$ 的熵,后半部分则就是交叉熵(Cross Entropy):$$ H(p,q) = - \sum_x p(x) \ln q(x) $$
实际应用中,如果将 $p(x)$ 和 $q(x)$ 分别作为真实值和预测值的概率分布,则由于前者的熵 $H(p)$ 是一个常数,因此:
$$ D_{KL}(p||q) \simeq H(p,q)$$
条件熵
给定随机变量 $X$ 和 $Y$ 及对应的概率分布 $p(x)$ 和 $p(y)$,则顾名思义条件熵定义如下:
$$
H(Y|X) = \sum_{x} p(x) H(Y|x) = \sum_{x} p(x) \sum_{y} p(y|x) \ln(p(y|x))
$$
说明:可理解为原数据集是 $Y$,条件(特征)$X$ 将原数据集分组后,新的一组数据集 $Y|X$ 的熵。从全概率公式角度理解,$\displaystyle\sum_{condition} p(condition) H(goal|condition)$.
用途:决策树
信息增益
分组使得熵减(数据纯度提升),熵减的大小就是信息增益。
$$
Gain(Y, X) = H(Y) - H(Y|X)
$$
用途:决策树 ID3 算法
信息增益率
分组后信息增益与条件的熵的比值。
$$
r(Y, X) = \frac{Gain(Y, X)}{H(X)}
$$
用途:决策树 C4.5 算法